수리적 사고력을 평가하는 기준으로 중요한 영역 가운데 하나가 기하학에 대한 이해와 응용이다. 기하학 학습을 통해 도형에 대한 정의 및 정리를 증명함으로써 도형을 이해하고, 평면 및 공간에 대한 예측과 창의력을 향상시킬 수 있기 때문이다.

다음은 중·고교 과정에서 배운 기초 도형인 삼각형의 오심(외심, 내심, 무게중심, 수심, 방심) 가운데 무게중심(또는 질량중심)을 활용하는 수리 논술 문제다.

제시문)

① 삼각형의 세 중선은 한 점에서 교차하는데, 이를 무게중심이라 한다. 한 꼭짓점에서 대변의 중점에 선분을 그어 만나는 점으로 꼭짓점과 대변의 중점을 이은 선분을 2:1로 내분한다.

② x-y 평면에서 삼각형의 세 꼭짓점 A(x₁, y₁) B(x₂, y₂) C(x₃, y₃)를 좌표평면에 나타낼 때,



선분 BC의 중점 M(x₂ + x₃/2, y₂ + y₃/2)과 한 꼭짓점 A(x₁, y₁)를 연결한 선분 AM을 2:1로 내분한 점 G(x₁ + x₂ + x₃/3, y₁ + y₂ + y₃/3)로 표현한다.

③ 무게중심과 두 꼭짓점으로 이루어지는 3개의 삼각형의 넓이는 같다. 일정한 질량을 갖는 삼각형인 경우 무게중심이 질량중심이 된다.

문제)

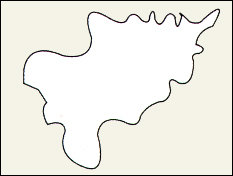
다음 두께 10cm, 한 변 길이 5m인 정사각형 모양의 철판으로 만들어진 맨홀이 있다. 오랫동안 사용해 녹이 슬어서 다음과 같은 형태로 남아 있다. 완전 교체하는 데 비용이 많이 들어서 녹슨 부분만 제거하고 보완하려고 한다. 새로 만들어서 채워야 하는 도형을 그리고, 만드는 데 드는 총 질량과 비용을 산정하시오.

또한 새로 만들어진 철판이 매우 무거워서 자석을 이용한 기중기를 활용하려고 한다. 단, 기중기는 질량중심에 자석을 연결하지 않으면 균형을 잃어서 사고가 나게 된다. 사고 없이 정확하게 새로 만들어진 도형을 채울 수 있는 방법을 제시하시오.(재료비 : 2만원/철 1kg, 철의 밀도 : 7.8×10³km/㎡) (정답 및 해설은 다음 호에 실립니다.)

550호 문제 정답 및 해설 해설 1) 단지 A(서쪽 끝에서 동쪽 10km 지점)와 관련된 편익을 계산해보자. ① A의 서쪽에 있는 모든 주민들은 이 관광단지를 이용할 것이 틀림없으므로 그들 각각에 대한 편익의 합계는 450억원이다(1인당 편익 4만5000원×100만 명). A의 동쪽에 있는 사람들은 반드시 A를 이용하지는 않을 것이기 때문에 A 편익의 합계는 1250억원이다(1인당 편익 2만5000원×500만 명). 따라서 A만 개발할 경우 총 편익은 1700억원이 된다. ② B(A에서 동쪽으로 20km 지점)단지가 개발된다면 20km 지점의 서쪽에 있는 주민은 A를 이용하고, 20km 동쪽에서 끝점(60km)까지는 B를 이용할 것이다. 이때 A의 편익은 900억원(4만5000원×100만 명+4만5000원×100만 명)이고, B의 편익은 1500억원(4만5000원×100만 명+3만5000원×300만 명)이다. ③ C단지가 A단지와 더불어 개발된다면 30km 지점 서쪽 주민은 A단지를, 동쪽 주민은 C단지를 이용할 것이다. 이때 A의 편익은 1250억원(4만5000원×100만 명+4만원×200만 명), C의 편익도 1250억원이 된다. ④ A, B, C단지가 모두 개발되는 경우 20km 서쪽 주민은 A단지로, 20~40km 사이 주민은 B단지로, 40km 동쪽 주민은 C단지를 이용하게 된다. 이때 A와 B, C 각각의 편익은 900억원(4만5000원×100만 명+4만5000원×100만 명)이 된다. 결론적으로 A단지와 관련된 편익은 다른 사업(B 또는 C)의 시행 여부에 따라 큰 차이를 보이며, 사업 간의 상호의존성이 매우 분명하다. 해설 2) 자본 제약은 없고(각 단지당 500억원) 해설 [1]에 의하면 각 사업간의 상호의존성이 뚜렷하므로 제시문 [2]의 수형도 가운데 네 번째 기준, 즉 상호의존적이며 자본 제약이 없는 경우는 NPV를 극대화하는 사업을 선택해 우선순위를 정한다. 다음은 A, B, C 지역에 관광단지를 개발했을 때 편익과 비용을 NPV로 나타내고 있다. 사업 편익 비용 NPV(단위 : 억원) 하지 않을 때 0 0 0 A 1700 500 1200 B 2100 500 1600 C 1700 500 1200 A,B 2400 1000 1400 A,C 2500 1000 1400 B,C, 2400 1000 1400 A,B,C 2700 1500 1200