552호 문제 정답 및 해설

부도심 A, B, C를 연결한 삼각형을 그린다. A점을 지나며 BC에 평행한 선을 긋고 B점을 지나며 AC에 평행한 선을, C점을 지나며 AB에 평행한 선을 그으면 서로 만나는 세 점 P, Q, R가 존재한다.

□ABCQ, □ARBC는 평행사변형이기 때문에 RA=BC=AQ이므로 부도심 A는 RQ의 중점이 된다.

□ABPC, □ARBC는 평행사변형이기 때문에 RB=AC=BP이므로 부도심 B는 PR의 중점이 된다.

□BCQA, □ABPC는 평행사변형이기 때문에 PC=AB=CQ이므로 부도심 C는 PQ의 중점이 된다.



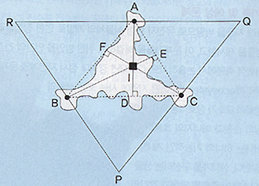따라서 P, Q, R점에 위성도시를 만들면 조건Ⅱ를 만족한다.

조건Ⅰ에 따라 시청의 위치는 세 위성도시 P, Q, R에서 같은 거리에 존재해야 하므로 세 위성도시 P, Q, R는 동일 원주상에 있고, 이 외접원의 중심에 시청이 위치해야 한다. 즉 시청에서부터 세 위성도시 P, Q, R까지의 거리는 외접원의 반지름이므로 모두 같다.

부도심 A점에서 대변 BC에 수선을 그어 만나는 점을 D라 하고, 부도심 B점에서 대변 AC에 수선을 그어 만나는 점을 E라 하고, 부도심 C점에서 대변 AB에 수선을 그어 만나는 점을 F라 하면 선분 AD, BE, CF의 교점은 I가 되고, 제시문 [1]의 정의에 따라 I점은 세 부도심 A, B, C를 꼭짓점으로 하는 삼각형 모형 기존 도시의 수심이 된다.

여기서 BC//RQ이고 BC⊥AD이면 RQ⊥AD이고, RA=AQ이므로 AD는 RQ의 수직이등분선이다. AB//PQ이고 AB⊥CF이면 PQ⊥CF이고, PC=CQ이므로 CF는 PQ의 수직이등분선이다. 마찬가지로 BE도 PR의 수직이등분선이다. 즉 AD, CF, BE의 모든 교차점 I는 제시문 [1]에 정의한 외심이 된다.

결론적으로 I점(시청의 위치)은 세 부도심 A, B, C점을 연결한 기존 도시의 수심이며, 동시에 새로운 위성도시 P, Q, R의 외심이 되고, 기존 도시의 세 부도심 A, B, C는 새로운 위성도시 P, Q, R로 이루어지는 삼각형의 각 면의 중점이 되므로 조건 Ⅱ를 만족한다.

그러므로 새로운 위성도시까지의 거리 IP=IQ=IR(I점은 외심), AR=AQ, BR=BP, CP=CQ를 만족하며 I점은 기존 도시 A, B, C의 수심 위치에 있다. 따라서 시청의 위치는 I점으로 하고 세 위성도시는 P, Q, R점에 만들면 된다.