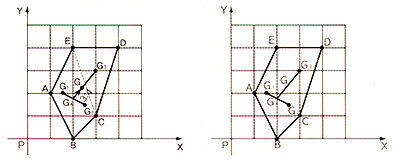
다음은 삼각형의 오심 중에서 외심 또는 수심이 어떻게 응용되는지 확인할 수 있는 문제입니다. 도형에 대한 이해가 충분하면 도시계획에도 응용할 수 있습니다.
제시문 1) 외심이란 삼각형 각 변의 수직이등분선의 교점을 말한다. 외심과 각 꼭짓점의 거리는 같다. 따라서 외심을 중심으로 원을 그으면 삼각형의 세 꼭짓점은 외접원의 원주상에 있다. 즉, 외심은 중심이 된다.
수심이란 삼각형의 한 꼭짓점에서 각 대변에 수선을 그어 만난 교점을 말한다. 평면도형에서 수심을 지나는 직선은 삼각형의 높이가 된다.
제시문 2) 도시가 자연 발생적으로 성장하여 인구가 1000만 명을 넘게 되면서 여러 가지 도시문제(주택 부족, 상하수도 시설미비, 교통체증, 교육문제 등)가 발생하게 되었다. 다음은 세 끝 지점에 부도심이 형성되어 있고 불규칙한 모습의 도시모형이 만들어졌다. 시민의 여론조사에 따르면 도심으로부터 이동거리와 교통수단이 거주지를 이전하는 가장 중요한 요소임이 확인되었다. 인구 분산을 위해 시청의 도시계획 위원장은 다음의 조건에 맞는 세 개의 위성도시(신도시)를 만들기로 했다.
1. 위성도시를 만들 때, 도심(시청 위치)에서 위성도시까지 거리가 같은 지역을 선정한다.
2. 부도심과 위성도시는 접근성(이동시간)이 같은 지점에 위치해야 인구 분산이 가능하다.(단, 모든 교통수단은 일정한 속력으로 이동한다.)
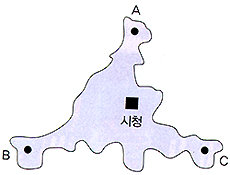 문제) 시청이 위치하는 지점을 도심이라 할 때, 위성도시는 도심으로부터 어느 정도에 위치해야 하는가? 또한 도심은 기존 도시 내에서 어느 지점에 있어야 하는지 시청의 위치를 정하고 그 이유를 서술하시오. (A, B, C점은 기존 도시의 부도심이다.)
문제) 시청이 위치하는 지점을 도심이라 할 때, 위성도시는 도심으로부터 어느 정도에 위치해야 하는가? 또한 도심은 기존 도시 내에서 어느 지점에 있어야 하는지 시청의 위치를 정하고 그 이유를 서술하시오. (A, B, C점은 기존 도시의 부도심이다.)
제시문 1) 외심이란 삼각형 각 변의 수직이등분선의 교점을 말한다. 외심과 각 꼭짓점의 거리는 같다. 따라서 외심을 중심으로 원을 그으면 삼각형의 세 꼭짓점은 외접원의 원주상에 있다. 즉, 외심은 중심이 된다.
수심이란 삼각형의 한 꼭짓점에서 각 대변에 수선을 그어 만난 교점을 말한다. 평면도형에서 수심을 지나는 직선은 삼각형의 높이가 된다.
제시문 2) 도시가 자연 발생적으로 성장하여 인구가 1000만 명을 넘게 되면서 여러 가지 도시문제(주택 부족, 상하수도 시설미비, 교통체증, 교육문제 등)가 발생하게 되었다. 다음은 세 끝 지점에 부도심이 형성되어 있고 불규칙한 모습의 도시모형이 만들어졌다. 시민의 여론조사에 따르면 도심으로부터 이동거리와 교통수단이 거주지를 이전하는 가장 중요한 요소임이 확인되었다. 인구 분산을 위해 시청의 도시계획 위원장은 다음의 조건에 맞는 세 개의 위성도시(신도시)를 만들기로 했다.
1. 위성도시를 만들 때, 도심(시청 위치)에서 위성도시까지 거리가 같은 지역을 선정한다.
2. 부도심과 위성도시는 접근성(이동시간)이 같은 지점에 위치해야 인구 분산이 가능하다.(단, 모든 교통수단은 일정한 속력으로 이동한다.)

|