1 강남 조 선생과의 두 번째 만남
 “내가 더 벌게. 열심히 공부해.”
“내가 더 벌게. 열심히 공부해.”
용만호 과장은 어젯밤 아내가 했던 말이 생각나 잠시 눈시울이 붉어졌다. 유치원 교사인 아내는 용 과장의 꿈과 도전을 진심으로 응원해주었다. ‘그래, 가족을 위해서라도 꼭 로스쿨에 갈 테야.’ 용 과장은 이렇게 의지를 다지며 강남 조 선생이 있는 H학원에 도착했다.
“선생님, 저 왔습니다. 용만호입니다.”
이윽고 강사휴게실 문이 열리면서 큰 키의 강남 조 선생이 해맑은 미소와 함께 모습을 드러냈다.
“오, 자네 왔나? 그래, 일주일 동안 공부는 많이 했는가?”
“오랜만에 하려니 힘이 들었지만, 아내의 적극적인 도움으로 열심히 할 수 있었습니다.”
“음, 그래. 좋은 아내를 두었구먼. 난 아직 미혼인데….”
“아, 그러세요? 별다른 뜻은 없었습니다. 전 그냥….”
“됐네. 그럼, 바로 수업이나 하세.”
2 간단한 계산 연습
“지난 시간에 자네가 풀어본 문제는 LEET 추리논증 영역의 추리 부분 중 논리게임이라는 유형의 문제였네. 그런데 추리 부분에는 논리게임 유형만 있는 게 아니야. 언어추리와 수리추리 유형도 있지. 그럼, 오늘은 그중에서 수리추리 유형을 배워보도록 하세.”
“선생님, 수리추리라는 건 수학을 말씀하시는 건가요? 전 수학엔 영 소질이 없어서요.”
“음, 그게…. 비슷하긴 한데 똑부러지게 수학이라고는 말할 수 없네. 그러니 겁먹지 말고 일단 간단한 퀴즈를 하나 풀어보겠나?”
“네, 열심히 하겠습니다. 제게 퀴즈를 내주십시오!”
용 과장은 손가락을 꼽아가며 퀴즈를 풀기 시작했다. ‘어렸을 때부터 계산엔 소질이 없어서 고등학교 시절에도 문과를 택했던 건데…. 쉬운 퀴즈라니까 어디 한번 차근차근 풀어보자. 이 대리는 첫 번째 근무일, 세 번째 근무일, 다섯 번째 근무일…, 박 대리는 첫 번째 근무일, 네 번째 근무일, 일곱 번째 근무일….’ 몇 분의 시간이 흘렀다.
“첫 번째 근무일, 일곱 번째 근무일, 열세 번째 근무일, 열아홉 번째 근무일, 이렇게 총 4일이군요!”
“이렇게 쉬운 걸 푸는 데도 그리 오래 걸리다니, 자네 정말 계산엔 소질이 없구먼. 하지만 여하튼 잘 풀었네. 자네도 파악했겠지만 이 퀴즈의 핵심은 ‘규칙성’을 찾아내는 것이네. 이 대리와 박 대리가 함께 지각한 날은 6일에 한 번씩 돌아오지. 그 규칙성만 찾아낸다면 답을 구하는 건 무척 쉽다네.”
“수리추리도 어렵지만은 않군요.”
“물론 실제 문제는 이보단 어렵다네. 하지만 많은 문제가 결국 여기에서 계산의 범위를 확장한 것에 지나지 않으니 절대 겁먹을 필요가 없네. 좁은 범위에서의 규칙성을 찾아낸 뒤 그걸 넓은 범위로 확장할 줄만 안다면 수리추리 유형의 상당 부분을 해결할 수 있을 것이네. 이와 관련한 더 자세한 얘기를 내 친구 하 선생에게 부탁해두겠네. 그 친구가 생긴 거와는 달리 아는 게 많으니 잘 배우도록 하게.”
“네, 알겠습니다.”
“그럼 자네, 내가 만든 진짜 문제를 풀어보겠나?”
3 강남 조 선생의 LEET 추리논증 -
규칙성을 찾아라!
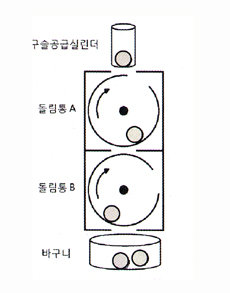
“자, 문제를 잘 풀어보았는가? 앞서도 얘기했듯 규칙성을 찾아내기만 한다면 이 문제의 답을 구하는 것은 무척이나 쉽다네. 그럼 나의 풀이를 보게나.”
“어때? 내 말을 잘 이해할 수 있겠는가? 이런 문제를 푸는 핵심은 아까 말한 대로 규칙성을 빨리 찾아내는 것이네. 이 문제에선 회전을 시작한 이후 4분 30초에 처음으로 바구니에 구슬이 전달되고, 이후 6분마다 규칙적으로 바구니에 구슬이 전달됨을 파악하는 것이었지. 자네도 그리 했는가?”
“저는 6분마다 A에서 B로 구슬이 전달되는 규칙성은 찾아냈는데, 그만 B가 바구니에 구슬을 전달하는 데 1분 30초가 더 소요된다는 점을 놓치고 말았습니다.”
“그래, LEET 문제에는 문제를 푸는 핵심요소 외에도 여러 가지 자잘한 함정이 있게 마련이지. 그런 함정을 피하는 법은 앞으로 꾸준히 공부하다 보면 자연스레 터득하게 될 걸세. 우선은 규칙성을 찾아내는 데 성공했으니 그것만으로도 훌륭하네. 오늘은 여기까지 하지.”
돌아오는 길에 용 과장은 규칙성에 대해 다시 한 번 생각했다. ‘그래, 공부도 규칙적으로 해야 더욱 능률이 오르겠지. 오늘은 집에 가서 학습시간표를 작성해야겠다.’ 용 과장의 발걸음은 힘이 넘쳤다. 그러나 그를 향해 시련의 그림자가 다가오고 있음을 그는 아직 알지 못했다. (합격의 법학원 ‘논리와비판 연구소’ 제공, 다음 호에 계속)

용만호 과장은 어젯밤 아내가 했던 말이 생각나 잠시 눈시울이 붉어졌다. 유치원 교사인 아내는 용 과장의 꿈과 도전을 진심으로 응원해주었다. ‘그래, 가족을 위해서라도 꼭 로스쿨에 갈 테야.’ 용 과장은 이렇게 의지를 다지며 강남 조 선생이 있는 H학원에 도착했다.
“선생님, 저 왔습니다. 용만호입니다.”
이윽고 강사휴게실 문이 열리면서 큰 키의 강남 조 선생이 해맑은 미소와 함께 모습을 드러냈다.
“오, 자네 왔나? 그래, 일주일 동안 공부는 많이 했는가?”
“오랜만에 하려니 힘이 들었지만, 아내의 적극적인 도움으로 열심히 할 수 있었습니다.”
“음, 그래. 좋은 아내를 두었구먼. 난 아직 미혼인데….”
“아, 그러세요? 별다른 뜻은 없었습니다. 전 그냥….”
“됐네. 그럼, 바로 수업이나 하세.”
2 간단한 계산 연습
“지난 시간에 자네가 풀어본 문제는 LEET 추리논증 영역의 추리 부분 중 논리게임이라는 유형의 문제였네. 그런데 추리 부분에는 논리게임 유형만 있는 게 아니야. 언어추리와 수리추리 유형도 있지. 그럼, 오늘은 그중에서 수리추리 유형을 배워보도록 하세.”
“선생님, 수리추리라는 건 수학을 말씀하시는 건가요? 전 수학엔 영 소질이 없어서요.”
“음, 그게…. 비슷하긴 한데 똑부러지게 수학이라고는 말할 수 없네. 그러니 겁먹지 말고 일단 간단한 퀴즈를 하나 풀어보겠나?”
“네, 열심히 하겠습니다. 제게 퀴즈를 내주십시오!”
|
용 과장은 손가락을 꼽아가며 퀴즈를 풀기 시작했다. ‘어렸을 때부터 계산엔 소질이 없어서 고등학교 시절에도 문과를 택했던 건데…. 쉬운 퀴즈라니까 어디 한번 차근차근 풀어보자. 이 대리는 첫 번째 근무일, 세 번째 근무일, 다섯 번째 근무일…, 박 대리는 첫 번째 근무일, 네 번째 근무일, 일곱 번째 근무일….’ 몇 분의 시간이 흘렀다.
“첫 번째 근무일, 일곱 번째 근무일, 열세 번째 근무일, 열아홉 번째 근무일, 이렇게 총 4일이군요!”
“이렇게 쉬운 걸 푸는 데도 그리 오래 걸리다니, 자네 정말 계산엔 소질이 없구먼. 하지만 여하튼 잘 풀었네. 자네도 파악했겠지만 이 퀴즈의 핵심은 ‘규칙성’을 찾아내는 것이네. 이 대리와 박 대리가 함께 지각한 날은 6일에 한 번씩 돌아오지. 그 규칙성만 찾아낸다면 답을 구하는 건 무척 쉽다네.”
“수리추리도 어렵지만은 않군요.”
“물론 실제 문제는 이보단 어렵다네. 하지만 많은 문제가 결국 여기에서 계산의 범위를 확장한 것에 지나지 않으니 절대 겁먹을 필요가 없네. 좁은 범위에서의 규칙성을 찾아낸 뒤 그걸 넓은 범위로 확장할 줄만 안다면 수리추리 유형의 상당 부분을 해결할 수 있을 것이네. 이와 관련한 더 자세한 얘기를 내 친구 하 선생에게 부탁해두겠네. 그 친구가 생긴 거와는 달리 아는 게 많으니 잘 배우도록 하게.”
“네, 알겠습니다.”
“그럼 자네, 내가 만든 진짜 문제를 풀어보겠나?”
3 강남 조 선생의 LEET 추리논증 -
규칙성을 찾아라!
|
“자, 문제를 잘 풀어보았는가? 앞서도 얘기했듯 규칙성을 찾아내기만 한다면 이 문제의 답을 구하는 것은 무척이나 쉽다네. 그럼 나의 풀이를 보게나.”
|
“어때? 내 말을 잘 이해할 수 있겠는가? 이런 문제를 푸는 핵심은 아까 말한 대로 규칙성을 빨리 찾아내는 것이네. 이 문제에선 회전을 시작한 이후 4분 30초에 처음으로 바구니에 구슬이 전달되고, 이후 6분마다 규칙적으로 바구니에 구슬이 전달됨을 파악하는 것이었지. 자네도 그리 했는가?”
“저는 6분마다 A에서 B로 구슬이 전달되는 규칙성은 찾아냈는데, 그만 B가 바구니에 구슬을 전달하는 데 1분 30초가 더 소요된다는 점을 놓치고 말았습니다.”
“그래, LEET 문제에는 문제를 푸는 핵심요소 외에도 여러 가지 자잘한 함정이 있게 마련이지. 그런 함정을 피하는 법은 앞으로 꾸준히 공부하다 보면 자연스레 터득하게 될 걸세. 우선은 규칙성을 찾아내는 데 성공했으니 그것만으로도 훌륭하네. 오늘은 여기까지 하지.”
돌아오는 길에 용 과장은 규칙성에 대해 다시 한 번 생각했다. ‘그래, 공부도 규칙적으로 해야 더욱 능률이 오르겠지. 오늘은 집에 가서 학습시간표를 작성해야겠다.’ 용 과장의 발걸음은 힘이 넘쳤다. 그러나 그를 향해 시련의 그림자가 다가오고 있음을 그는 아직 알지 못했다. (합격의 법학원 ‘논리와비판 연구소’ 제공, 다음 호에 계속)
|