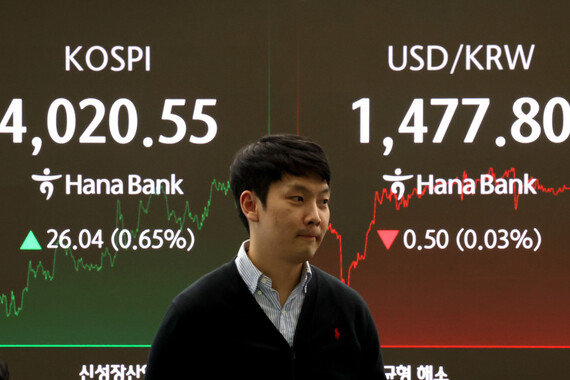
시점에 움직임을 도입해 역원근법으로 그린 서구의 그림들. 하나의 점에 시선을 고정한 후 평면에 투사해 그리는 기존의 원근법과는 다르게 표현돼 있다.
‘경험비판론’으로 유명한 오스트리아 물리학자 에른스트 마흐의 말이다. 이 말 속에는 서구 원근법이라는 낯선 문법에 익숙하지 않은 눈이 느끼는 당혹감이 표현되어 있다. 파노프스키의 말대로 서구의 원근법은 그저 ‘상징형식’, 말하자면 3차원 공간을 2차원의 평면에 투사하는 한 가지 규약에 불과하다. 그럼 공간을 다르게 표상하는 또 다른 규약은 없을까? 왜 없겠는가. 애초에 약속을 달리하면 얼마든지 서구의 원근법과는 다르게 그릴 수 있다.
‘하나의 움직이지 않는 눈으로 본다. 그렇게 본 장면을 평면에 투사한다.’ 이것이 서구의 원근법을 지탱하는 두 가지 규약. 이 중 어느 하나를 포기하면 각각 다른 투시법들이 얻어진다. 가령 선원근법의 규약과 달리 장면을 곡면이나 사면에 투사하면 마니에리스모와 바로크 시대에 유행하던 왜곡상(anamorphosis)이 얻어질 것이다. 반면 시점을 고정시킨다는 규약을 깨고 시점에 움직임을 도입하면 위 그림에서 보는 것처럼 서구의 것과는 정반대로 뒤집어진 ‘역원근법(obratnaya perspektiva)’이 탄생한다.
소실점이 아래로
그것은 시점을 고정시키지 않았기 때문이다. 가령 책상을 볼 때 우리는 정면만 보지 않고, 걸음을 옮겨 왼쪽 측면도 보고 오른쪽으로 돌아가 우측면도 확인한다. 이렇게 책상을 왼쪽에서 본 모습, 오른쪽에서 본 것을 하나로 합치면 한 장의 그림에 왼쪽 면과 오른쪽 면이 동시에 보이게 된다. 그러면 당연히 책상의 앞쪽은 짧게, 뒤쪽은 길게 묘사될 것이다. 하나의 시점만을 사용하는 서구 원근법과 달리 러시아의 역원근법은 이렇게 두 개의 시점을 하나로 합친 운동지각(Kinasthesia)을 구현한다.
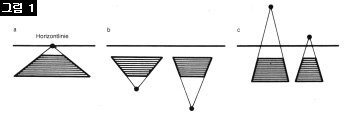
이 규약의 차이가 전혀 다른 투시법을 낳는다. 이를 도표로 나타내보자. 그림 a는 우리에게 익숙한 서구 원근법의 원리. 여기서 사물의 좌우로 흐르는 사선들(orthogonal lines)은 결국 위쪽의 수평선(horizontal line)에서 만난다. 반면 b는 러시아 역원근법의 원리를 나타낸다. 여기서 사선들은 외려 대상의 아래쪽에 소실점을 만들어낸다. 즉 소실점이 사물의 위에 있는 수평선에 걸리면 서구 원근법, 사물의 아래쪽에 떨어지면 러시아의 역원근법이라고 보면 된다.
그럼 c는? 소실점이 위에 있어 언뜻 서구 원근법처럼 보인다. (실제로 원근법이 확립되기 전에는 서구에서도 종종 저런 투시법을 사용했다.) 하지만 저 역시 역원근법의 하나다. 여기서 소실점은 수평선 너머 한참 위쪽에 있다. 이는 대상의 앞이 약간 짧고 뒤가 조금 길게 묘사되기 때문에 일어나는 현상이다. 이렇게 앞을 짧게, 뒤를 길게 묘사하는 것은 역원근법의 원리. 따라서 언뜻 보기에 선원근법 같아도 c는 어디까지나 역원근법이다. 이를 ‘위장한 역원근법’이라 부른다. 러시아 장인들은 b와 c를 교차로 사용한다.
직선을 곡선으로
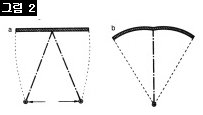
예수가 앉아 있는 의자의 테두리가 수평, 수직으로 모두 둥글게 굽어 있다. 앞서 얘기한 역원근법의 효과다. 그런데 그 옆에 있는 성모 마리아의 의자를 보라. 똑같은 의자인데도 여기서는 테두리가 직선으로 묘사되어 있다. 무엇이 이런 차이를 낳았을까? 그것은 예수의 이미지가 벽화인 반면 마리아의 이미지는 부조이기 때문이다. 회화는 2차원 평면의 예술이기에 ‘투시법’이 필요하지만, 아무리 평평해도 부조는 3차원 예술인 조각이므로 굳이 투시법이 필요하지 않다는 얘기다.

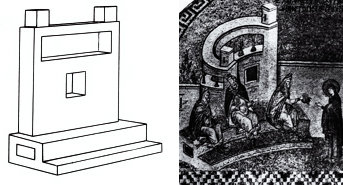

어느 출판사에 이에 관한 글을 보냈더니 편집부에 있는 이들이 내 말을 안 믿는다. 저 구조물이 애초에 굽은 것을 그린 게 아니냐는 거다. 여기서 저절로 한 가지 물음이 떠오른다. 직선을 곡선으로 그린다면 애초에 곡선으로 굽은 구조물은 어떻게 그려야 할까? 러시아의 장인들은 해답을 갖고 있었다. 처음부터 말굽처럼 생긴 구조물을 한 번 더 굽힐 때는 아래 그림에서 보듯 굽은 벽을 두 쪽으로 잘랐다. 즉, 둥글게 굽은 벽이 중간에 뭉텅 잘려 있으면 그 구조물은 애초부터 굽어 있었던 것으로 해석하면 된다.
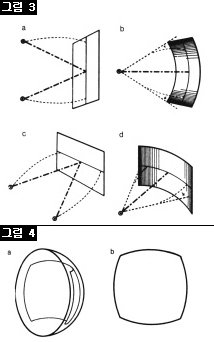
그럼 동그라미는 어떻게 그려야 할까? 원형을 떨어져서 보면 타원형으로 보인다. 타원형의 윗부분을 한 번 굽히면(b), 곡률이 상승해 거의 반원처럼 될 것이다(c). 반면 타원형의 아랫부분은 반대로 휘어 있기에 그것을 안쪽으로 굽히면(d) 외려 평평하게 펴질 것이다(e). 이 둘을 위아래로 합쳐놓으면 어떻게 될까? 결국 반원형의 도형이 얻어질 것이다(f). 따라서 러시아 성화에서 종종 보는 반원형의 탁자는 실제로는 원형이라고 해석해야 한다.
러시아 장인들이 제멋대로 그림을 그린 게 아니다. 그들 나름대로 엄격한 투시법을 적용하고 있었다. 파노프스키의 말대로 서구 원근법은 유일하게 과학적인 재현방식이 아니다. 그 역시 문화적으로 상대적인 하나의 ‘상징형식’일 뿐이다. 러시아의 뒤집어진 원근법은 파노프스키의 말을 입증해주는 강력한 증거다.