
2010년 서울 남산골 한옥마을에서 열린 ‘남산골 전통축제’ 참가자들이 윷놀이를 즐기고 있다.
도·개·걸·윷·모 적절한 확률
우리나라 사람이라면 누구나 아는 이 윷놀이는 우리 민족이 오래전부터 즐겨온 전통놀이다. 원래 윷놀이할 때 말을 놓는 윷판은 요즘 많이 쓰는 네모 모양이 아니라 원 모양이었다. 독립운동가이자 역사학자였던 단재 신채호 선생에 따르면 윷놀이의 ‘도’ ‘개’ ‘걸’ ‘윷’ ‘모’는 고조선 때 다섯 부족을 의미한다. 외부에서 침입한 적과 싸우러 나갈 때 왕을 배출한 부족을 가운데 두고, 네 부족을 둘러 배치한 진(陣) 모양을 본뜬 것이 바로 윷판이라는 것이다. 도, 개, 걸, 윷, 모는 각각 가축인 돼지, 개, 양, 소, 말을 뜻한다고 한다. 윷놀이할 때 윷판에서 한 칸만 가는 도는 발걸음 느린 돼지를, 그리고 한 번에 다섯 칸을 훌쩍 가는 모는 말을 의미한다.
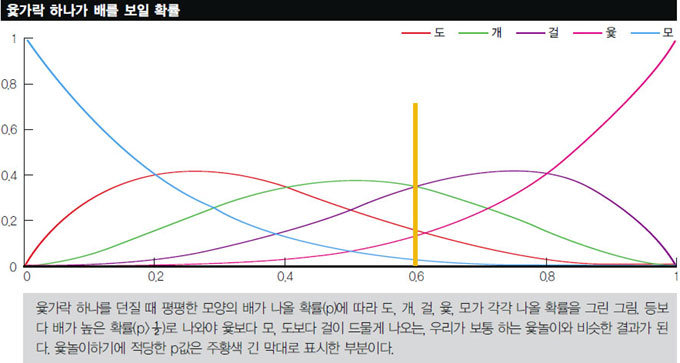
윷가락은 바닥에 떨어지면서 둥근 모양인 등을 보이거나 평평한 모양의 배를 보인다. 윷가락 하나가 배를 보일 확률을 p라 하면 간단한 수학 계산으로 도, 개, 걸, 윷, 모가 각각 어떤 확률로 나올지 어렵지 않게 알 수 있다.
우리 말에 ‘모 아니면 도’라는 게 있는 걸 봐도 알 수 있듯, 다섯 가운데 가장 좋은 건 한 번에 가장 멀리 갈 수 있는 모다. 따라서 모는 도, 개, 걸, 윷, 모 중 가장 드물게 나오는 것이 맞으리라. 만약 ‘p=1/2’로 윷가락의 배와 등이 나올 확률이 같아지면 도와 걸, 그리고 윷과 모는 모두 똑같은 확률로 나오게 돼 우리가 보통 하는 윷놀이와 양상이 달라진다. 윷놀이를 할 때는 보통 개나 걸이 자주 나오고, 모는 윷보다 드물게, 또 윷이 도보다 드물게 나오는 것이 그럴 듯하니 ‘p=3/5’정도가 적당하다는 것을 알 수 있다. 즉 윷가락 하나를 여러 번 던지면 다섯 번에 세 번꼴로 배를 보이는 것이 놀이에 적당한 윷가락이다(그래프 참조).
프로 도박사도 매번 못 이겨

단원 김홍도의 풍속화. 민속학자들은 이 그림에서 등장인물 들이 즐기는 놀이가 윷놀이라고 설명한다.
몬테카를로는 카지노로 유명한 휴양 도시 이름이다. 지중해에 면한 아름다운 작은 나라 모나코에 있다. 몬테카를로는 필자 같은 통계물리학자에게는 무척이나 익숙한 이름이기도 한데, 널리 쓰이는 컴퓨터를 이용한 수치 계산 방법에 바로 이 이름이 붙어 있기 때문이다. 몇 년 전 국제통계물리학회에 참석했다 학회 장소에서 멀지 않은 모나코를 방문해 몬테카를로 카지노 앞에서 성지순례하는 기분으로 단체 사진을 찍은 일도 있다. 정장을 입지 않은 탓에 복장불량이란 이유로 카지노에 들어가지는 못했다(대규모 국제학회에 참석할 때도 정장을 말쑥이 차려입고 넥타이까지 매는 물리학자는 거의 없다).
왜 과학자들의 계산 방법에 엉뚱하게 몬테카를로라는 이름이 붙었을까. 카지노에서 돈을 걸고 도박하면 아무리 프로 도박사라도 매번 돈을 따지는 못한다. 이처럼 같은 일을 반복해도 매번 결과가 달라지면 원하는 결과가 나올 ‘확률’을 아는 것이 중요하다. 다른 사람에게 속임수를 써서 돈을 따는 나쁜 사람이 아니라면, 도박사들은 자신이 가진 패가 상대방을 이길 확률을 정확히 알아야 결국 승부에서 이길 수 있다. 간단한 경우라면 계산이 쉽지만 참여자가 여럿이고, 매번 벌어지는 상황이 무궁무진한 복잡한 게임이라면 그 확률을 정확히 계산해내는 건 어려운 일이다. 고교 수학 교과서에 나오는 한 줌밖에 안 되는 문제를 제외하면 현실에서 벌어지는 일의 확률을 정확히 계산하는 것은 대부분 불가능하다.
이럴 때 해볼 수 있는 게 뭘까. 바로 몬테카를로 카지노에서처럼, 주사위를 굴리거나 마구잡이로 카드를 섞어 게임하듯 무작위적인 수많은 경우에 대해 실험하고 그 결과를 이용해 확률을 계산하는 것이다. 컴퓨터는 이처럼 단순 무식한 일을 수없이 반복하기에 가장 적절한 장치다. 컴퓨터를 이용해 몬테카를로 방법으로 계산한다는 말은 곧 풀고자 하는 문제에 맞는 컴퓨터 프로그램을 만든 뒤 컴퓨터로 하여금 엄청나게 여러 번 똑같은 일을 마구잡이로 반복하게 하는 것을 뜻한다.
예를 들어보자. 바늘만 있으면 원주율(파이·π)을 구할 수 있다는 말을 들어봤는지. ‘뷔퐁의 바늘(Buffon’s needle)’이라 부르는 이 문제에서는 일정한 간격으로 금을 그은 종이 위에 바늘을 마구잡이로 던져서 바늘이 금에 걸쳐지는 경우가 얼마나 되는지 세어보는 게 필요하다. 그 확률을 이용하면 원주율을 구할 수 있다. 종이와 바늘 그리고 손으로 하는 몬테카를로 계산이라고 할까.
‘주간동아’ 911호에서 필자가 소개한 프로야구 일정표를 가장 공정하게 짜는 방법에 대한 연구에서도 비슷하게 컴퓨터를 이용했다. 일정표를 이렇게 바꿔보고 저렇게 바꿔보는 마구잡이 과정을 수십만 번 반복한 뒤, 그중 가장 효율적인 일정표를 찾는 몬테카를로 방법을 이용한 것이다.
이제 독자도 눈치챘겠지만, 윷놀이를 할 때 잡기와 업기 중 어떤 전략을 쓰는 편이 더 유리할까에 대한 답을 얻으려고 필자와 학생들이 택한 것이 바로 컴퓨터를 이용한 몬테카를로 방법이다. 계산의 편의를 위해 윷판을 단순화해 갈림길이 없는 윷판을 생각했다. 보통 쓰는 윷판에서 바깥쪽 네모 테두리 길만 따라간다고 생각하면 된다. 또 말이 많아지면 복잡해지기 때문에 한 편마다 말을 두 개씩만 사용하도록 했다. 실제 윷놀이보다 단순하다는 한계가 있긴 하지만, 이 계산을 통해 업기와 잡기 두 전략 사이에 의미 있는 승률 차이가 있음을 발견할 수 있었다.
먼저 시작하는 것이 유리

통계물리학자들이 널리 사용하는 ‘몬테카를로 방법’은 카지노에서 주사위를 굴리거나 마구잡이로 카드를 섞듯 무작위적인 수많은 경우에 대해 실험하고, 그 결과를 이용해 확률을 계산하는 방법을 뜻한다.
컴퓨터를 이용해 무려 10억 번 계산한 끝에 얻은 결과를 바탕으로 필자가 독자에게 드리는 조언은 간단하다. 일단 윷놀이는 다른 편보다 먼저 시작하는 것이 유리하고, 또 업기와 잡기 중 고민될 때는 일단 상대편 말을 잡는 것이 낫다. 이 연구 결과는 박혜진, 심하성, 그리고 조항현 박사와 함께 한국물리학회지(Journal of Korean Physical Society)에 논문으로도 게재했다.
사실 윷놀이에 대한 이번 글은 내년 설쯤 주간동아에 소개하려고 마음먹고 있던 주제였다. 제철도 아닌데 윷놀이 얘기를 독자가 뜬금없이 읽게 된 이유는 지금쯤이 ‘물리학자 김범준의 이색 연구’ 연재를 마치기에 적당한 때라는 생각을 했기 때문이다. 연재를 마치는 이유는 전혀 이색적이지 않다. 안타깝게도 ‘이색 연구’로 소개할 연구 밑천이 거의 다 떨어졌기 때문이다.
세어보니 이번이 벌써 스무 번째 글이다. 유시민은 모든 것이 변하니 “같은 책을 두 번 읽는 사람은 없다”고 했다. 같은 글을 두 번 쓸 수 있는 사람도 없다. 아니 어쩌면 ‘글을 쓴 후에도 여전히 같은 사람일 수 있는 사람은 없다’가 더 적절한 듯하다. 스무 번의 기회를 준 주간동아와 연재 글을 읽어준 모든 분께, 또 대부분 글의 첫 독자였던 아내에게 감사의 마음을 전한다.

















