
2010년 8월 풍산 류씨 후손들이 경북 안동시 풍천면 하회마을 내 대종가인 양진당에서 하회마을의 유네스코 세계문화유산 등재를 조상에게 알리는 고유제를 지내고 있다.
필자는 고등학생 시절 눈 쌓인 운동장에서 덜덜 떨면서 월요일 아침조회가 시작되기를 기다린 적이 있다. 그사이 누가 먼저 시작했는지, 전교생이 좌우 두 패로 나뉘어 눈을 뭉쳐 반대편 쪽으로 하늘 높이 던지며 지겨운 조회가 시작되기 전 짧은 시간을 즐겁게 보냈다. 코끝이 싸한 겨울날, 파란 겨울 하늘을 뒤덮던 하얀 눈뭉치들(더위가 좀 가셨는지).
한국 성씨 300개 vs 일본은 13만여 개
그런데 놀랍게도 눈뭉치는 대부분 사람에게 맞지 않고 운동장에 떨어졌다. 사실 남산에서 돌 던지면 누가 맞을까라는 속담이 얘기하려는 것은 ‘남산에서 던진 돌이 사람에게 맞았다면 그 사람은 누구일까’라는 조건부 확률 문제다.
속담을 끄집어낸 이유는 어려운 확률 얘기를 하자는 게 아니다. 바로 성씨 얘기를 하려는 것이다. 우리나라에는 고유한 문화적 특징이 많다. 그 가운데 다른 어느 나라에서도 찾을 수 없는 특징이 우리나라에 있는 모든 성씨를 종이 한 장도 안 되는 분량에 다 적을 수 있다는 것이다(표 참조). 우리나라 성씨는 300개 정도밖에 되지 않는다. 이웃나라 일본엔 13만여 개 성씨가 있다.
혹시 80대 20 법칙을 들어봤는가. 사회에서 발견되는 많은 통계에서 20% 정도의 사람이 전체 80%의 부를 차지하는 것을 일컫는 말이다. 우리 사회의 부와 소득 분포만 80대 20 법칙을 보이는 것이 아니다. 한 기업의 판매상품 가운데 20%가 전체 매출의 80%를 차지한다거나, 한 회사 사원의 20%가 회사 전체 이익의 80%를 만드는 것 등 다양한 예가 있다(회사원의 80%는 아마도 자신이 그 20%에 속한다고 생각할 것이다).
마찬가지 셈법을 ‘표’에 있는 우리나라 성씨에 적용해보자. 상위 22개 성씨(즉 22÷285(전체 성씨)×100=7.7·약 8%)가 전체 인구의 80% 정도를 차지하므로 우리나라 성씨 분포는 80대 20이 아닌 80대 8 법칙을 따른다. 즉 상위 성씨에 집중된 정도가 아주 심한 편이다. 물리학자들은 이런 이야기를 말보다 그래프로 그리는 것을 좋아한다.
상위는 엄청 많고 하위는 엄청 적고
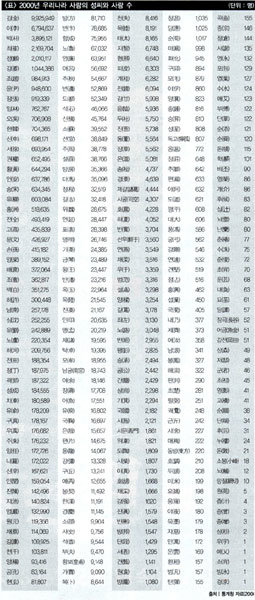
‘그래프1’을 보자. 가로축에는 가장 많은 성씨인 김씨를 1위, 그다음인 이씨를 2위, 박씨를 3위 하는 식으로 각 성씨의 순위를 놓고, 세로축에는 각 성씨를 가진 사람이 몇 명인지를 놓아 그린 그래프다. 순위가 뒤로 갈수록 그 성씨를 가진 사람의 수가 줄어들다 보니 그래프는 왼쪽 위에서 오른쪽 아래로 내려가는 모양이다. 세로축은 가로축과 달리 1, 10, 100, 1000처럼 10배가 늘어날 때마다 한 눈금 간격이 되도록 그린 것에 유의하자(이런 그래프를 로그 축척(log scale)으로 그렸다고 한다). 그림 가운데 부분을 보면 넓은 범위에 걸쳐 직선처럼 보이는 부분이 있는데, 이는 우리나라 성씨의 순위빈도(rank-frequency) 그래프가 지수함수(exponential function)꼴을 갖는다는 의미다. 어려운 말은 다 빼고 간단히 설명하면, 우리나라 성씨 분포는 상위 성씨는 엄청 많고, 하위로 내려갈수록 그 성씨를 갖는 사람 수가 급격히 줄어든다는 것이다.
‘그래프 2’를 보자. 필자가 몇몇 도시의 전화번호부를 학생들과 함께 살펴보고, 한 대학 재학생들의 성씨를 분석해 만든 그래프다. 가로축에는 한 집단에 몇 명이 있는지, 세로축에는 그 집단에서 서로 다른 성씨가 몇 개 발견됐는지를 그렸다. ‘그래프 1’과 달리 이번에는 가로축을 1, 10, 100식으로 10배씩 늘어나는 눈금으로 그렸다.
이 그래프는 사람 수가 늘어남에 따라 한 집단에서 발견되는 성씨가 아주 천천히 증가하는 것을 보여준다(정확히 말하면 성씨 수는 사람 수의 로그함수꼴로 증가한다). 우리나라에서는 인구가 10배가 돼도 성씨는 지금보다 기껏해야 몇십 개 정도만 늘어날 것으로 기대할 수 있다. 사실 그래프의 가장 왼쪽 점은 필자가 강의한 수강생을 대상으로 조사한 결과다. 독자들도 기회가 되면 자신이 속한 집단의 사람 수와 그 집단에서 발견되는 성씨 수를 구해 그 결과를 ‘그래프 2’에 겹쳐 그려보라. ‘그래프 2’의 직선에서 크게 벗어나지 않는 결과를 얻을 게 거의 확실하다.
이처럼 우리가 사회현상의 거시적 패턴에서 벗어나는 것은 쉽지 않다. 그렇다고 거시적 패턴의 존재가 우리 각자의 자유의지와 모순되는 것은 결코 아니다. 오히려 한 사람 한 사람이 본인의 성씨와 무관하게 자유롭게 집단을 형성하고, 자유의지에 따라 거주지를 결정하기 때문에 이와 같은 거시적 패턴이 드러난다고 필자는 생각한다.
자세히 설명하긴 쉽지 않지만 ‘그래프 1’과 ‘그래프 2’는 같은 정보를 다르게 그린 것일 뿐 수학적으로는 동등하다. 즉 엄청나게 빨리 감소하는 ‘그래프 1’의 함수꼴과 엄청나게 천천히 증가하는 ‘그래프 2’의 함수꼴은 동전 앞뒷면처럼 밀접하게 얽혀 있다. 다른 나라의 성씨를 예로 들어 그린다면 ‘그래프 1’의 직선은 우리나라보다 엄청 천천히 감소하고 ‘그래프 2’의 직선은 우리나라보다 엄청 빨리 증가해 우리나라와 ‘엄청’ 다르게 될 것이다. 여기서 ‘엄청 다름’의 의미는 그래프의 함수꼴 자체가 다르다는 뜻이다(일본을 포함한 대부분의 다른 나라에서는 둘 모두 멱함수다. 우리나라의 경우 ‘그래프 1’은 지수함수, ‘그래프 2’는 로그함수꼴이다). “우리가 아는 아인슈타인 박사는 딱 그 한 사람이지만, 김 박사는 여러 명”이라는 말은 누구나 아는 우리나라와 다른 문화권의 차이를 수학적으로 좀 더 정교하게 표현한 것이라고 생각하면 된다.
이처럼 독특한 우리나라 성씨의 분포 모양이 과거에는 어땠을까. 과거의 성씨 분포를 살피는 것이 얼핏 어려울 듯 보이지만 불가능한 일도 아니다. 유서 깊은 집안의 족보를 살펴보면 된다. 물론 한 집안 족보에 기재된 남자는 당연히 성이 모두 같다. 그러나 우리나라 족보에는 그 집안에 시집온 여자들의 생년 및 성씨 본관(관향)도 함께 기재된 경우가 많으니 이를 이용하면 된다.
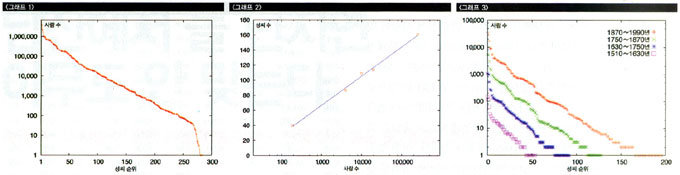
몇몇 집안의 족보만 살펴봐도 몇백 년 전 성씨 분포를 미뤄 짐작할 수 있다. ‘그래프 3’은 필자가 전산화된 족보 자료 10개를 이용해 그 집안들에 시집온 여자 수십만 명의 성씨 분포를 ‘그래프 1’과 같은 방법으로 그려본 것이다. 과거로 거슬러 올라갈수록 족보에 기재된 사람 수가 적어서 그래프가 아래로 이동하긴 하지만, 그래프의 함수꼴은 500년 동안 거의 변화가 없다는 것을 알 수 있다. 조선 초까지 거슬러 올라가도 우리나라 성씨 분포는 지금과 비슷했다는 말이다.
정리해보자. 우리나라 성씨 분포는 예나 지금이나 다른 나라와 많이 다르다. 사람 수가 늘어나도 그 안에서 발견되는 성씨 수는 아주 천천히 증가하고, 김·이·박 같은 극소수의 성씨를 가진 사람이 아주 많으며, 상대적으로 나머지 성을 가진 사람 수는 적다.
그렇다면 우리나라는 왜 이처럼 다른 나라와 성씨 분포가 다를까. 그 이유는 우리나라에서는 새로운 성씨가 만들어지거나 존재하던 성씨가 없어지는 일이 거의 생기지 않았기 때문이다. “지금까지 위에서 얘기한 내용이 사실이 아니면 성을 갈겠다”고 필자가 말한다면 우리나라 사람은 그것이 무슨 뜻인지 누구나 이해한다. 우리 문화에서 ‘성을 간다’는 것은 정상인이라면 거의 상상할 수도 없는 금기사항이니까. 예나 지금이나 바로 이 특성이 우리나라 성씨 분포가 다른 나라와 비교해 독특한 이유다.
성씨와 관련해 우리나라만의 독특한 면이 또 있다. 하나는 ‘본관’과 성씨를 합해 한 사람의 가계를 파악할 수 있다는 것이고, 다른 하나는 우리나라 사람은 서양과 비교해 ‘이름’이 무척 다양하다는 것이다. ‘본관’과 ‘이름’에 대한 얘기는 다음 기회에 살펴보겠다.

















