한 번의 칭찬이 누군가의 인생을 바꾼다

인생은 비극이다. 잘 안 되던 것이 저절로 잘 되지는 않는다. 열심히 노력한다고 다 잘 되는 것도 아니다. 하지만 일단 잘 못하던 것에 빠져봐야 잘할 수 있는 길이 열린다. 지난해 손주은 메가스터디 회장으로부터 들은 일화다.

공포의 학거북산 문제

초등학생 시절 필자를 괴롭히던 ‘학거북산’ 문제를 극복하자 수학과 친구가 될 수 있었다. [GETTYIMAGES]

“제가 처음 본 카퍼레이드가 초등학생 때 경남 창원군(현 창원시) 출신 박봉주 마라토너의 전국체전 우승 기념 퍼레이드였어요. 그날의 감동으로 마라토너가 되겠다 다짐하고 초등학교 3학년 때 한동안 운동장을 매일 15바퀴(3000m)씩 달렸습니다. 중2 가을에는 사라예보 세계탁구선수권대회에서 이에리사를 중심으로 한 한국 선수들이 중국을 이기고 처음으로 우승해 전국 카퍼레이드가 펼쳐졌고 고향 국도를 지나갔어요. 태극기를 들고 환영하러 나갔죠. 그 후 마침 중2 겨울 시골 동네에 탁구장이 생겨 두 달 동안 매일 6시간씩 탁구를 쳤습니다.”

손 회장은 “몰입과 중독 사이에서 늘 헤매던 인생이 여기까지 온 것 같다”고 회상했다. 그는 “대한민국에서 강의 시간으로는 1등이라고 생각한다”며 “주당 60시간 강의를 25년 이상 했고 22시간 30분이라는 연속 강의 기록도 갖고 있다”고 말했다. 물론 모든 사람이 이렇게 할 필요는 없지만 한국 경제성장 배경에는 이런 측면도 작용했다는 생각이 든다.

필자의 경우는 어땠을까. 과거에 2년 동안 트라우마를 겪었던 수학 문제가 있다. “학과 거북이 있는데 머리 합은 5, 다리 합은 14다. 이때 학과 거북이 몇 마리씩 있을까”라는 문제였다. 이른바 ‘학거북산’으로 불리는 수학 문제로, 초등학교 5학년 내내 필자를 괴롭혔다. 비교적 어려운 문제에 속했고 시험에도 항상 나왔다. 당시 문제 설명이 잘 이해되지 않았다. 게다가 건방지게도 푸는 방식마저 마음에 들지 않았다. 당시 필자는 마음에 들지 않는 이 문제를 푸는 것을 거부했다. 객관식 문제로 나오면 답을 찍었고, 주관식 문제로 나오면 답란에 아무 숫자나 써넣었다.

세월이 흘러 중학교에 입학하기 전 잠시 학원에서 영어와 수학을 배웠다. 방정식을 배웠는데 마침 같은 문제가 나왔다. 그런데 문제 푸는 방식이 완전히 달랐다. 학과 거북의 숫자를 각각 x, y라고 가정한 후 푸는 방식이었다.

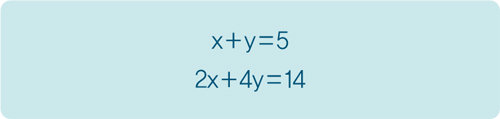이 문제를 풀기 위해선 우선 첫째 식을 ‘x=5-y’로 변형해야 한다. 이를 둘째 식에 대입하면 ‘2(5-y)+4y=14’가 된다. 이 식을 정리하면 ‘10-2y+4y=14’가 되며, y가 2라는 사실이 도출된다. 마지막으로 이를 첫째 식에 대입하면 x가 3이라는 사실도 알 수 있다. 학 3마리, 거북 2마리가 정답인 것이다.

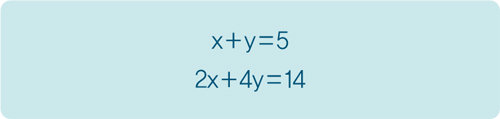
필자는 이 풀이 방식이 무척 신기하고 마음에 들었다. 특히 “모르는 것을 x라고 하자”는 시작이 아주 세련돼 보였다. 항상 마음을 불편하게 했던 짐을 벗어버리게 되자 그렇게 시원할 수 없었다. 수학에 재미를 붙이고 열심히 공부했고, 한 달 후 수학시험에서 예상외로 만점을 받았다.

초등생은 원시적으로 수학 문제 푸는 게 좋아

수업시간에 문제를 열심히 풀고 있는데 뒤에서 두툼한 손이 머리에 얹어지는 것이 느껴졌다. 수학 선생님은 필자에게 “시험을 잘 봤던데, 수학에 소질이 있나 봐. 학교에서 반 1, 2등 하니?”라고 물었다. 당시 책을 많이 읽기는 했지만 학교 성적은 좋지 않았다. 수학 선생님의 따듯한 칭찬은 수학을 더 열심히 하게 만들었고, 그 결과 수학을 아주 잘하고 또 좋아하게 됐다. 한 과목을 잘하게 되니 다른 과목 성적도 저절로 올라갔다. 중고교 시절 수학은 나를 지켜주는 친구 같은 존재였다. 수학 문제를 푸는 것 자체를 즐겁게 여기니 문제를 들여다보면 저절로 풀렸다. 한 번의 칭찬이 인생을 바꾼 것이다.

특강에서 이 얘기를 하면 아예 초등학생에게 연립방정식을 가르치는 것이 어떠냐는 질문이 나온다. 그러나 초등학생에게는 원시적으로 수학 문제를 푸는 방법을 가르치는 것이 더 좋아 보인다. 가령 대화하면서 이 문제를 푼다고 생각해보자. 초등학생에게 같은 문제를 말하면서 풀어보라고 하면 이렇게 대화가 흘러갈 것이다.

“학과 거북의 머리 합이 다섯이니까 모두 5마리잖아요. 학이 1마리면 거북 4마리, 학이 2마리면 거북 3마리, 학이 3마리면 거북 2마리, 학이 4마리면 거북 1마리. 그런데 학이 5마리일 수도 있겠네요. 학이 1마리도 없을 수도 있고요. 전부 따져보면 되죠. 학이 3마리고 거북이 2마리면 학은 다리가 3×2 해서 6개이고, 거북은 다리가 4×2 해서 8이네요. 야호! 다리 합이 14다. 이게 정답이구나. 학 3마리와 거북 2마리 맞죠?”

“그래 잘했다. 학과 거북을 합쳐 5마리니까 하나씩 따져봐도 되지만, 수가 커져서 학과 거북의 머리를 합하면 25, 다리를 합하면 80이라면 어떻게 할래.”

“이전 방식대로라면 26번 따져봐야 되겠네요. 이번엔 다리부터 해볼까요. 다리가 80개니까 거북만 있다고 하면 80÷4 해서 20마리예요. 그런데 25마리 중 나머지가 학이니까 학이 5마리고, 다리 총합이 90개라는 얘긴데 이건 답이 아니죠. 거북이 19마리 있다고 보면 다리 개수는 88이에요. 규칙이 있네요. 거북이 1마리 줄고 학이 1마리 늘어날 때마다 다리 수가 2씩 줄어들잖아요. 다리 수 합이 90에서 80이 되려면 거북을 5마리 줄이면 되겠네요. 그러니까 20-5 해서 거북이 15마리고 학은 25-15 해서 10마리예요.”

고등학교에서 배운 행렬을 사용하면 더 깔끔하게 문제를 풀 수 있다. 특히 식이 많아지면 이 방식이 훨씬 편하고 직관적이다. 3x=2에서 x=2÷3을 구하는 것과 1차 연립방정식의 관계 역시 마찬가지다. 생각해보면 물리학·경제학에서 쓰는 연립방정식도 근본 원리는 초등학생 때 접하는 학거북산 문제에서 출발한다.

_{김재준 교수는…
서울대 경제학과를 졸업하고 미국 프린스턴대에서 경제학 박사학위를 받았다. 국민대 경상대학장, 국민대 도서관장과 박물관장, 한국예술경영학회 회장을 역임했으며 현재 국민대 국제통상학과 교수로 재직하고 있다.}