사람의 몸무게가 표준보다 더 나가는지 아닌지 판단할 때 보통 몸무게를 키의 제곱으로 나누는 ‘체질량지수(BMI)’를 이용한다. 연구 결과 사람의 몸무게는 생후 약 1년을 기준으로 키의 제곱에 비례하는 것으로 나타났다.
물리학의 눈으로 이 풍경을 본다. 다른 무엇보다 ‘생선살이 많다’는 건 무슨 뜻일까. 필자 주변에 있는 물리학자는 이처럼 별 게 다 궁금한 사람들이다. 지금 밥상 위 자기 앞에 놓인 생선이 같은 길이의 표준적인 생선에 비해 살이 많은지 적은지를 어떻게 알 수 있을까.
BMI 23~30이면 과체중
생선이 아니라 사람이라면 몸무게가 표준보다 더 나가는지 아닌지 판단할 때 보통 ‘체질량지수(body-mass index·BMI)’를 이용한다. 몸무게를 kg 단위로 적고, 키는 m 단위로 적은 다음 몸무게를 키의 제곱으로 나누면 나오는 값이다. 키가 170cm고 몸무게가 70kg이라면 70을 1.7의 제곱인 2.89로 나눈 값인 24가 그 사람의 체질량지수다(필자의 몸 수치는 아니다. 필자 키는 마누라도 모르는 극비사항이다).
참고로, 보통 BMI가 23~30이면 과체중, 30 이상이면 비만이라고 얘기한다. 키가 달라도 사람의 체질량지수는 고만고만하게 비슷한 값을 갖는다(이 글에서 ‘고만고만하게 비슷한 값을 갖는다’는 말은 BMI의 확률분포가 종 모양의 정규분포를 따른다는 뜻이다).
자, 그럼 밥상에 오른 굴비도 마찬가지로 체질량지수를 계산해 그 값이 가장 큰 것을 ‘가장 살찐 굴비’라고 판단하면 될까. ‘누가 살찐 굴비를 먹을까’에서 시작한 필자의 궁금증은 이제 더 깊어진다. 사람의 체질량지수는 왜 하필 몸무게를 키의 제곱으로 나눌까. 키의 세제곱으로 나누는 것이 더 자연스럽지 않을까 하는 쪽으로 뻗어가는 것이다. 왜 그런지 살펴보자. 물리학자가 이런 얘기를 할 때는 보통 다음과 같은 말로 시작한다.
“자, 사람 몸을 한 변 길이가 h인 정육면체라고 하자.”
현실에 존재하지 않는 이 반듯한 사람 부피는 h3이다. 세제곱 수가 나오는 이유는 우리가 사는 공간이 3차원이라 모든 물체가 가로, 세로, 높이 등 3개 공간 차원을 갖기 때문이다. 몸의 무게는 부피에 비례하고, 비례상수인 밀도는 누구나 거의 같다. 따라서 정육면체 사람의 몸무게를 부피 h3으로 나누면 사람은 대부분 고만고만한 값을 가질 것이다.
좀 이상하지 않은가. 앞에서 체질량지수를 계산할 때는 몸무게를 키의 세제곱(h3)이 아니라 제곱(h2)으로 나눠야 그 값이 고만고만하다고 했는데, 정육면체 사람의 경우는 몸무게를 키의 세제곱으로 나눠야 값이 고만고만하다는 것이다. 왜 다를까. 당연히 그 이유는 사람을 가로, 세로, 높이가 모두 h인 정육면체로 볼 수 없기 때문이다. 이처럼 물리학자는 가정을 만들고 그로부터 얻어지는 결론을 살펴본 뒤 그게 좀 이상하면 다시 처음으로 돌아가 가정을 고민한다.

필자 지인이 잡은 노래미. 물고기는 비교 대상이 없으면 실제 크기를 알기 어렵다.
이 사각기둥 사람의 몸무게는 부피인 ha2에 비례하므로 보통 계산하듯 키의 제곱으로 몸무게를 나눠(ha2÷h2) 체질량지수를 구하면 그 값은 a2÷h에 비례하게 된다. 보통 계산하는 방법으로 구한 체질량지수가 고만고만하다는 것의 의미는 이제 사람은 대부분 a2÷h 값이 고만고만하게 나온다는 뜻이 된다.
이로부터 ‘왜 키가 큰 사람은 날씬해 보일까’에 대한 답도 쉽게 얻을 수 있다. 사각기둥 사람의 허리둘레는 a에 비례하니 허리둘레의 제곱을 키로 나누면 사람 대부분에게는 a2÷h와 마찬가지로 키가 크든 작든 이 값이 비슷하게 나온다.
여기서 쉬운 문제 하나. 체질량지수가 비슷한 두 사람이 있고 한 사람이 다른 사람보다 키가 2배 크다고 하자. 키가 큰 사람의 허리둘레는 키가 절반인 사람의 몇 배가 될까. 만약 2배라고 답했다면 앞의 글을 다시 찬찬히 읽어볼 것. 맞는 답은 2배보다 작은 약 1.4배(√2)다(이래야 두 사람의 a2÷h 값이 같다).
따라서 키가 큰 사람은 날씬해 보이고(키가 2배 큰데 허리둘레는 1.4배만 크니까), 키가 작으면 통통해 보인다. 이로부터 얻을 수 있는 또 다른 흥미로운 결론이 있다. 아무런 배경이나 비교 대상 없이 사람만 찍은 사진을 봐도 우리는 그 사람의 키가 어느 정도인지 짐작할 수 있다(극단적으로 막 걸음마를 시작한 아기가 서 있는 사진을 떠올려볼 것. 그 사진에서 아기 키가 성인보다 훨씬 작다는 것은 재보지 않아도 누구나 알 수 있다. 믿기지 않으면 아이에게 만세를 불러보라고 할 것. 아이의 귀여운 사진을 보면 만세 부른 팔의 손끝이 머리 정도까지만 올라간다. 성인 가운데 그런 사람은 없다).
월척 물고기 크기의 비밀
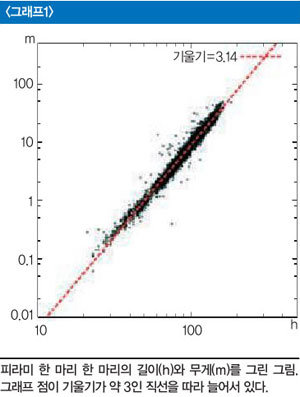
‘그래프1’은 필자의 생물학 분야 공동연구자인 전태수 교수와 송미영 박사가 보내준 자료를 이용해 민물고기인 피라미 한 마리 한 마리의 무게와 길이를 평면 위에 그린 것이다. 그래프의 점 대부분이 기울기가 3 정도인 직선을 따라 분포하는 것을 확인할 수 있다. 물고기의 체질량지수는 물고기 무게를 길이의 세제곱으로 나눠 구하면 된다는 뜻이다. 앞의 노래미 사진에서 얘기했듯 물고기의 경우엔 사진만 갖고 물고기의 원래 크기를 알기 힘들다. 엄청난 크기의 오징어가 깊은 바다에 살고 있다고 하자. 이처럼 큰 오징어라도 사진을 찍어 나란히 놓으면 어물전 작은 꼴뚜기와 별로 다르게 보이지 않을 것이다.
생후 400일 이전 아이는 물고기?
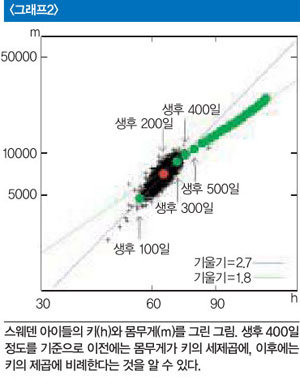
예를 들어 100~200일에 속한 모든 아이의 몸무게와 키 자료를 가리키는 점은 검은색으로 표시했다. 이 점들의 평균을 물리학의 질량 중심처럼 구하면 빨간색 점이 된다. 녹색 점들은 생후 일수를 기준으로 아이들을 나눈 뒤 평균을 내 그린 것이다. 아이들이 자라면서 키와 몸무게가 늘어나는 것을 볼 수 있다. 흥미롭게도 생후 400일 정도를 기준으로 이전과 이후 점들이 늘어선 직선의 기울기가 달라진 것을 볼 수 있다. 400일 무렵 이전에는 기울기가 2.7로 3에 가깝고, 이후에는 1.8로 2에 가깝다.
이 그래프의 직선 기울기는 체질량지수를 구할 때 몸무게를 키의 몇 제곱으로 나눠야 할지를 정하는, 그 ‘몇’에 해당하는 숫자다. 즉, 400일 정도 이전 아이의 체질량지수는 마치 물고기처럼 키의 세제곱으로 구하는 것이 맞고, 이후에는 키의 제곱으로 구하는 것이 더 맞다는 것을 보여준다.
그 이유는 뭘까. 왜 아이의 체질량지수 계산법이 400일 무렵을 기준으로 변할까. 또 왜 사람의 체질량지수 계산법은 물고기와 다를까. 필자가 생각하는 답은 바로 ‘사람은 두 발로 걷기 때문’이다. 보통 아이는 돌이 지난 후 걷는다. 엄마 배 속에서는 마치 물고기처럼 헤엄친다. 아이가 태어난 후 제대로 된 ‘걷는 사람’이 되는 시점이 바로 ‘한 돌’을 지날 때다. 우리 선조가 ‘첫돌’을 크게 축하한 이유가 바로 이 때문은 아닐까.

















